사각형, 원 이라면 (x,y) 좌표를 쉽게 구할 수 있다.
하지만 구는 (x,y,z) 좌표를 구하기가 쉽지 않았다.
구면좌표계
정의 : 3차원 구의 형태를 나타낼 수 있는 좌표 표현법으로, 거리r과 두개의 각으로 표현되는 좌표계.
좌표 (r,θ,φ)는 다음과 같이 정의 된다. 주어진 점을 P라 하자.
|
■ r : 원점으로부터 P까지의 거리 ■ θ: z축의 양의 방향으로부터 원점과 P가 이루는 직선까지의 각 ■ φ : x축의 양의 방향으로부터 원점과 P가 이루는 직선을 xy평면에 투영시킨 직선까지의 각 |

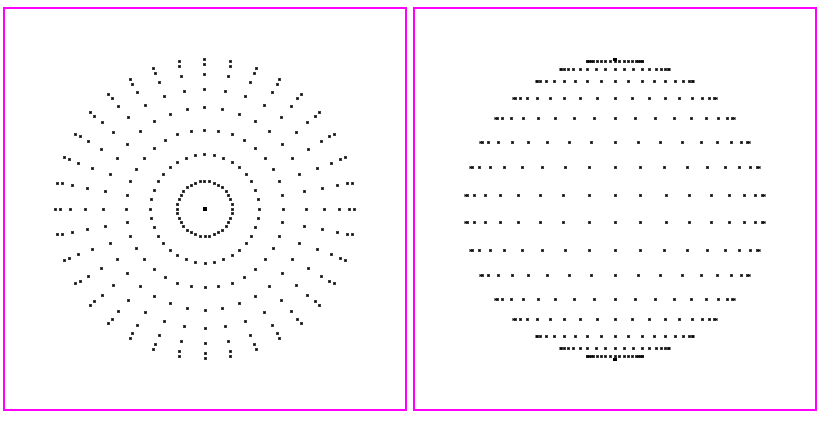
위 그림을 통해 θ, φ를 구하고, 이를 역변환하여 x,y,z를 구한다.
구면좌표계의 경우는 좌표값에 따라 한 점을 여러 좌표가 가리키는 경우가 있으므로, 각 변수의 범위를 보통 아래와 같이 제한한다.
r >0
0 ≤ θ ≤ π
0 ≤ φ ≤ 2π
좌표변환
다른 3차원 좌표계로 변환하는 공식은 다음과 같다.
직교좌표계에서 구면좌표계로 변환시

구면좌표계에서 직교좌표계로 변환시

전체소스
<!DOCTYPE html>
<head>
<meta charset="utf-8">
<style>canvas { border:2px solid magenta; }</style>
</head>
<body>
<canvas id="canvas1" width="400" height="400"></canvas>
<canvas id="canvas2" width="400" height="400"></canvas>
<script>
window.onload = function() {
var ctx1 = document.getElementById("canvas1").getContext("2d");
var ctx2 = document.getElementById("canvas2").getContext("2d");
var No_theta=36; //가로 둘레에 36개를 그린다.
var No_phi=18; //세로 둘레에 18개를 그린다.
var center = { x: 200, y: 200 }; //중심점
var Radius = 150; //반지름
var delta_theta = 2 * Math.PI / No_theta; // 2*PI(360도) / 쪼갤겟수
var start_phi = -Math.PI / 2.0; // 반구씩 계산함
var delta_phi = Math.PI / (No_phi - 1); // PI(180도) / 쪼갤겟수
var theta, phi, obj = {};
for (var j = 0; j < No_phi; j++) {
for (var i = 0; i < No_theta; i++) {
theta = i * delta_theta;
phi = start_phi + j * delta_phi;
obj.x = Math.floor( Radius * Math.cos(phi) * Math.cos(theta) );
obj.y = Math.floor( Radius * Math.cos(phi) * Math.sin(theta) );
obj.z = Math.floor( Radius * Math.sin(phi) );
ctx1.strokeRect( center.x+obj.x , center.y+obj.y, 1,1);
ctx2.strokeRect( center.x+obj.y , center.y+obj.z, 1,1);
}
}
}
</script>
</body>
</html>
참고 : https://ko.wikipedia.org/wiki/%EA%B5%AC%EB%A9%B4%EC%A2%8C%ED%91%9C%EA%B3%84
'프론트엔드 개발 놀이터 > etc' 카테고리의 다른 글
| 구글(Google) 검색에 내 사이트 등록하는 방법 (0) | 2020.02.24 |
|---|---|
| 홈페이지 제작 후 할 일 – 검색엔진, 포털 등록 (0) | 2020.02.24 |
| 원의 좌표 공식 (원 그리기) - js (0) | 2020.02.13 |
| 삼각함수 공식 정리 (0) | 2020.02.12 |
| 위도 경도 찾기 (0) | 2020.02.11 |
